논리연산
논리연산이란 다른 비트들이 표현하는 내용으로 새로운 비트를 만들어내는 것을 말한다.
예시)
'밥을 먹었으면 tv를 보고 그렇지 않으면 책을 읽어라'는
밥을 먹었는가에 대한 비트대답 예(true), 아니오(false)에 대한 결과에 따라 다른 행동을 하게 할 수 있다.
불리언대수
불리언대수란 비트에 대해 사용할 수 있는 연산규칙의 집합을 말한다.
불리언연산자의 종류
| NOT , AND , OR , XOR |
1. NOT: 논리적 반대
- NOT(거짓) = 참
2. AND: 둘 이상의 비트 중 하나라도 거짓이면 거짓
- (첫번째 비트: 참), (두번째 비트: 참) = 참
- (첫번째 비트: 참), (두번째 비트: 거짓) = 거짓
- (첫번째 비트: 거짓), (두번째 비트: 참) = 거짓
- (첫번째 비트: 거짓), (두번째 비트: 거짓) = 거짓
3. OR : 둘 이상의 비트 중 하나라도 참이면 참
- (첫번째 비트: 참), (두번째 비트: 참) = 참
- (첫번째 비트: 참), (두번째 비트: 거짓) = 참
- (첫번째 비트: 거짓), (두번째 비트: 참) = 참
- (첫번째 비트: 거짓), (두번째 비트: 거짓) = 거짓
4. XOR : 배타적OR로 둘다 달라야 참
- (첫번째 비트: 참), (두번째 비트: 참) = 거짓
- (첫번째 비트: 참), (두번째 비트: 거짓) = 참
- (첫번째 비트: 거짓), (두번째 비트: 참) = 참
- (첫번째 비트: 거짓), (두번째 비트: 거짓) = 거짓

드모르간의 법칙
1800년대 영국 수학자 오거스터스 드모르간은 불리어대수에 법칙을 추가했는데 그게 드모르간의 법칙이다.
a AND b = NOT(NOT a OR NOT b)
코딩으로 표현하면
a || b === !(!a && !b)
a && b === !(!a || !b)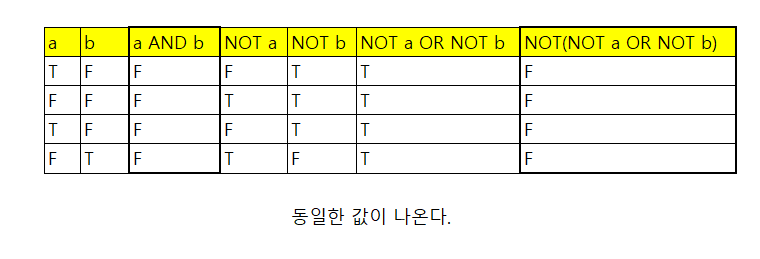
NOT을 충분히 사용하면 AND 연산을 OR로 바꿀 수 있고
반대로 OR 연산을 AND로 바꿀 수 있음을 보여준다.
예시)
* 긍정적인 논리라는 뜻의 '정논리', 부정적인 논리라는 뜻의 '부논리'로 구분
배가 고프고 졸릴 때에는 잠을 잠을 잔다 => 정논리
배가 고프지 않고 졸리지 않을 때에는 잠을 자지 않는다 => 부논리
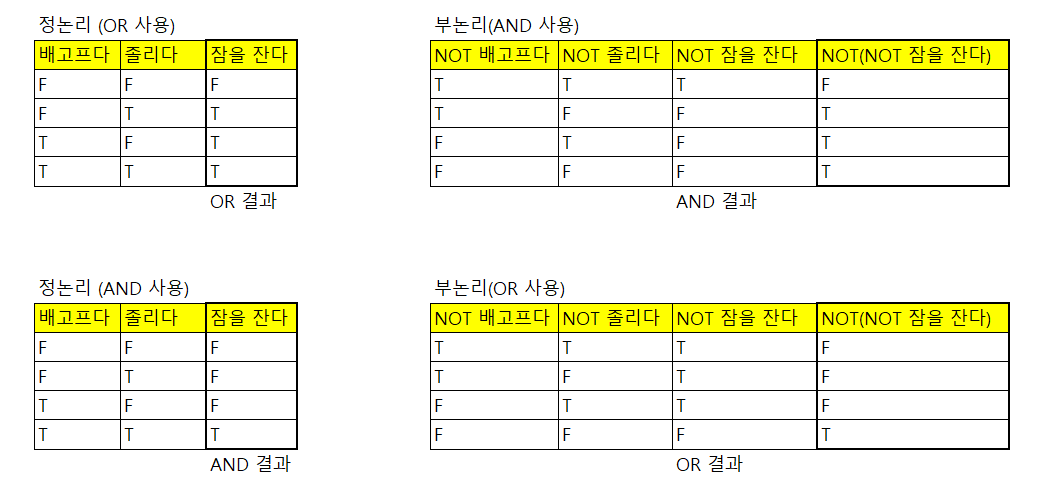
OR을 사용한 정논리와 NOT(AND)를 사용한 부논리가 같다.
반대로 AND를 사용한 정논리와 NOT(OR)를 사용한 부논리가 같다.
'비전공자 스터디노트' 카테고리의 다른 글
| 실수를 표현하는 방법 (0) | 2022.01.05 |
|---|---|
| 정수를 비트로 표현하는 방법 (2) | 2022.01.04 |
| 문자언어와 비트 (0) | 2022.01.02 |
| 컴퓨터 내부의 언어 체계_언어란 무엇인가? (0) | 2022.01.01 |
| 한 권으로 읽는 컴퓨터 구조와 프로그래밍_ 스터디 시작 (0) | 2022.01.01 |



